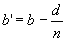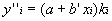




Признаю – название получилось запутанным и неинформативным. Может оно хоть интригует!.. попытаюсь описать суть задачи в тексте.
Предположим, Вы планируете развитие какой-нибудь балансовой статьи. Пускай, это будут среднемесячные остатки на счетах клиентов. Вы долго мучались, изучая сезонность, стараясь сделать рост менее линейным и приближенным к реальности.
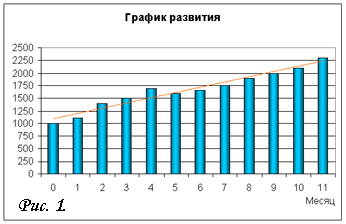
А теперь я попробую сформулировать эту задачу более формально. Есть процесс с некоторым трендом (как на рис. 1). Нужно изменить наклон тренда, не меняя начального значения, и главное – формы развития (как на рис. 2).
Что же мы в данном случае должны сделать. Для начала нужно определить начальный линейный тренд. Тренд представляет собой линейную функцию x – номер месяца (либо другое более подходящее значение) начиная с 0. Я подчеркнул это потому, что если вы пронумеруете месяцы, начиная с 1, в итоге кроме наклона тренда получите и его общее снижение, т.е. первое значение окажется ниже;
y – фактические значения показателя в каждом месяце;
n – количество месяцев (или значений x).
Полученные после вычисления параметры позволят определить теоретическое (усредненное) значение тренда в каждом месяце.
Форма развития записана. Теперь можно заняться наклоном тренда. За угол наклона отвечает параметр b. Уменьшая его, мы уменьшаем угол по отношению к горизонтальной оси и наоборот.
Параметр уравнения тренда a остается без изменений. Новые теоретические значения можно рассчитать по формуле Рассчитав новые значения, вы сможете увидеть наклоненный тренд с полностью сохраненной формой графика, присутствующей в предыдущем в начальном графике.
Возможно, мои объяснения не слишком подробные, но мне кажется, что сама методика слишком легка, чтобы ее описывать более понятно. Конечно, решать эту задачу лучше всего с помощью компьютера. Более того, я сделал это за вас. В следующем файле-примере описанная вышек методика полностью реализована. Этот файл можно вполне использовать в качестве полноценного инструмента планирования. Пользуйтесь на здоровье!
Итак, приходит печальный момент демонстрации результатов планирования начальству, а Вам говорят примерно такую фразу: «Ну это ты загнул! Куда ж оно вырастет до пи… миллионов! Минимум на миллион меньше делай. А сначала вроде все верно…».
Указание может быть интерпретировано по-другому, но суть остается одна! Как правило, первые месяцы просматриваются гораздо лучше, поэтому Ваше мнение и мнение начальства по поводу первых 2-х месяцев, скорее всего, сойдутся. Но чем дальше в год, тем толще амбиции!



Теперь нужно получить отклонения от среднего тренда. Мы как бы сделаем фотографию формы развития процесса, включая все сезонные колебания. Для этого рассчитаем коэффициенты относительного отклонения фактического значения от теоретического в каждом месяце:
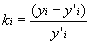
Для того чтобы наклонить тренд и в результате получить последнее значение на d меньше, чем было до наклона, нужно вычислить новый параметр b’ по формуле: